Błąd obciążenia i wariancji - kompromis

Autor sekcji: dr Filip Wójcik

Niniejszy podrozdział przedstawia kolejny, bardzo istotny aspekt uczenia maszynowego, jakim jest kompromis pomiędzy błędem obciążenia i wariancji. Jest to jedna z najczęściej przywoływanych zależności w uczeniu maszynowym, która ma kluczowe znaczenie w procesie budowy modeli predykcyjnych.

Kompromis między obciążeniem a wariancją

W kontekście uczenia maszynowego, mówimy o kompromisie między obciążeniem a wariancją (ang. bias-variance tradeoff). Jest to jedno z kluczowych pojęć, które pozwala zrozumieć, jakie są dwa najczęściej pojawiające się błędy, popełniane przez modele.

Zacznijmy jednak od obrazu, który mówi więcej niż tysiąc słów. W kontekście kompromisu między obciążeniem a wariancją bardzo często przywołuje się analogię z tarczami strzelniczymi - taką, jak pokazana poniżej.

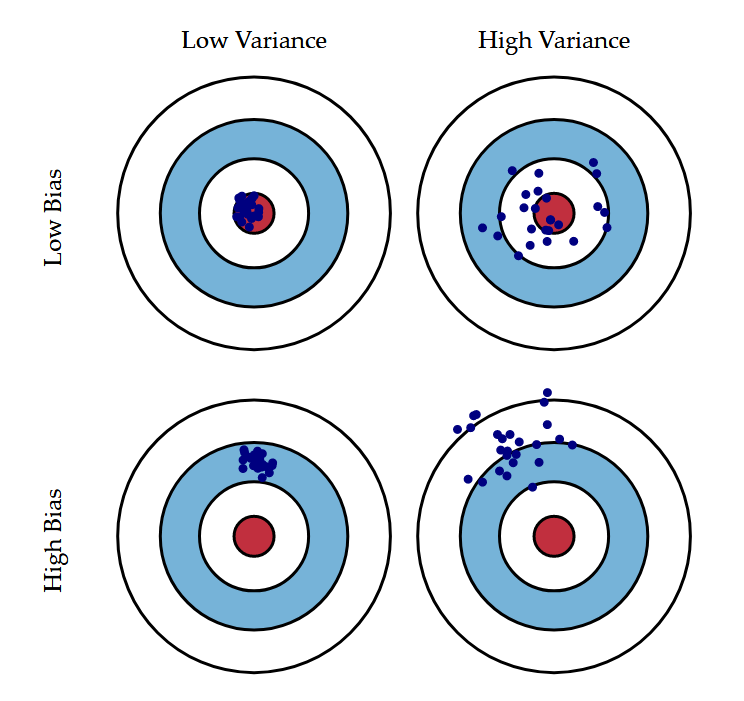
Rys. 3 Obciążenie i wariancja - targe strzelnicze. Źródło: Devopedia - bias variance tradeoff

Na rysunku widzimy cztery hipotetyczne sytuacje:

1. Low bias + low variance / niskie obciążenie + niska wariancja - wszystkie trafienia układają się blisko centrum i nie są zbyt rozproszone. Oznacza to, że model jest w stanie dobrze przewidywać wartości, a jego trafienia są stabilne.

2. Low bias + high variance / niskie obciążenie + wysoka wariancja - trafienia są rozproszone, ale układają się blisko centrum. Oznacza to, że model jest w stanie średnio i co do zasady dobrze przewidywać wyniki, ale jego trafienia są niestabilne.

3. High bias + low variance / wysokie obciążenie + niska wariancja - trafienia są skupione, ale daleko od centrum. Oznacza to, że model ma problem z trafnym przewidywaniem w sposób systematyczny, ale jego trafienia są stabilne.

4. High bias + high variance / wysokie obciążenie + wysoka wariancja - najgorsza możliwa sytuacja. Trafienia są rozproszone i daleko od centrum. Oznacza to, że model ma problem z trafnym przewidywaniem w sposób systematyczny, a jego trafienia są niestabilne.

Każdy strzał do tarczy strzelniczej możemy traktować jako pojedyncze przewidywanie modelu. W praktyce, chcemy, aby nasz model był w stanie przewidywać wyniki w sposób stabilny i trafny, co niestety nie zawsze jest możliwe.

Czynniki sprzyjające błędowi obciążenia i wariancji

W praktyce obserwujemy często następującą zależność:

1. Im większa złożoność modelu - tym większa wariancja i mniejsze obciążenie. Wynika to z faktu, że bardziej skomplikowany model (np. sieć neuronowa) jest w stanie reprezentować niezwykle złożone zależności w danych, ale jednocześnie jest bardziej podatny na zmiany w danych uczących i może to doprowadzić do niestabilnych predykcji.

2. Im mniejsza złożoność modelu - tym mniejsza wariancja i większe obciążenie. Prostsze modele (np. regresja liniowa) są mniej podatne na zmiany w danych uczących, ale jednocześnie mają ograniczoną zdolność do reprezentowania złożonych zależności w danych.

Mając na uwadze powyższe elementy, możemy teraz zdefiniować obciążenie, wariancję i kompromis między nimi.

Błąd obciążenia modelu / Prediction bias

Obciążenie modelu to systematyczny błąd, który wynika z uproszczeń, jakie wprowadzamy w procesie uczenia. W praktyce oznacza to, że jego predykcja mijają się z wartością docelową. [AMMIL12] [Dom12]

Błąd wariancji modelu / Prediction variance

Wariancja modelu to miara tego, jak bardzo różnią się predykcje modelu, w zależności od zmian w zbiorze uczącym. Wysoka wariancja oznacza, że model często zmienia swoje decyzje, w zależności od niewielkich wahań w danych. [AMMIL12] [Dom12].

Kompromis między obciążeniem a wariancją / Bias-variance tradeoff

Kompromis między obciążeniem a wariancją to pojęcie, które mówi o tym, że w praktyce gdy zwiększamy złożoność modelu - redukując jego błąd obciążenia, zwiększamy jednocześnie wariancję. Zmniejszając złożoność modelu - zwiększamy błąd obciążenia, ale jednocześnie zmniejszamy wariancję. Bardzo rzadko możliwe jest jednoczesne zmniejszenie obydwu rodzajów błędu. [AMMIL12] [Dom12] [SW17]

Zanim przejdziemy do praktycznych przykładów, zdefiniujemy powyższe elementy w postaci formalnej.

Mając dany konkretny zestaw danych \(\mathbf{X}_i\) lub skrótowo \(\mathbf{X}\),oraz docelowych etykiet/kategorii (czyli nasze Pojęcie docelowe, którego szukamy) \(\mathbf{y} = f(\mathbf{X})\), zbiór wielu takich zestawów: \(\mathcal{D}=\{(\mathbf{X}_1, \mathbf{y}_1), (\mathbf{X}_2,, \mathbf{y}_2), \dots, (\mathbf{X}_k, \mathbf{y}_k) \}\), model uczenia maszynowego \(h\), dokonujący predykcji na tym zbiorze \(\hat{y} = h(\mathbf{X})\), możemy zdefiniować błąd modelu jako sumę błędu obciążenia, błędu wariancji i błędu nieredukowalnego w kontekście.

Zaczynamy od definicji naszej funkcji kosztu - posłużymy się błędem średniokwadratowym:

\[S = (y - \hat{y})^2\]

Posługując się wzorem skróconego mnożenia \((a+b)^2 = a^2 + 2ab + b^2\) oraz przekształceniem algebraicznym polegającym na dodaniu i odjęciu tej samej wartości - w tym przypadku wartości oczekiwanej predykcji (czyli średniej predykcji) dla wszystkich zbiorów danych, możemy zapisać:

(6)\[\begin{split} \begin{aligned} S &= (y - \hat{y})^2 \\ &= (y - E_{\mathcal{D}}[\hat{y}] + E_{\mathcal{D}}[\hat{y}] - \hat{y})^2 \\ &= (y - E_{\mathcal{D}}[\hat{y}])^2 + 2(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y}) + (E_{\mathcal{D}}[\hat{y}] - \hat{y})^2 \\ \end{aligned} \end{split}\]

W równaniu (6) powyżej traktujemy człony

1. \(y - E_{\mathcal{D}}[\hat{y}]\) jako a we wzorze skróconego mnożenia

2. \(E_{\mathcal{D}}[\hat{y}] - \hat{y}\) jako b we wzorze skróconego mnożenia i potem korzystamy z własności wzoru skróconego mnożenia.

Ponieważ uczenie modelu jest procesem stochastycznym, musimy uśrednić ten wynik dla wielu różnych zbiorów danych. Do tego służy operator wartości oczekiwanej \(E_{\mathcal{D}}[\cdot]\). Zanim to zrobimy, zwróćmy uwagę, że:

1. \(y\) nie jest zależne od zbioru danych - to deterministyczna funkcja, Pojęcie docelowe, które chcemy przewidzieć - ono jest raz na zawsze ustalone. Tym samym \(E_{\mathcal{D}}[y] = y\)

2. \(E_{\mathcal{D}}[\hat{y}]\) to średnia predykcja modelu na wielu różnych zbiorach danych. To jest nasze obciążenie - czyli błąd, który wynika z uproszczeń, jakie wprowadzamy w procesie uczenia. Ta część nie będzie stałą, ale będzie silnie zależeć od specyfiki zbioru danych.

3. Z ogólnej własności operatora własności oczekiwanej wiemy, że: \(E[E[x]] = E[x]\).

4. Z definicji wariancji, wiemy, że jest ona definiowana jako: \(Var(x) = E[(x - E[x])^2]\)

Zobaczmy teraz, jak możemy zdefiniować błąd obciążenia i wariancji w kontekście powyższego równania.

(5)\[\begin{split} \begin{aligned} E_{\mathcal{D}}[S] &= E_{\mathcal{D}}[(y - \hat{y})^2 ] \\ &= E_\mathcal{D}\left[(y - E_{\mathcal{D}}[\hat{y}])^2 + 2(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y}) + (E_{\mathcal{D}}[\hat{y}] - \hat{y})^2\right] \\ &= E_{\mathcal{D}}[(y - E_{\mathcal{D}}[\hat{y}])^2] + E_{\mathcal{D}}[2(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y})] + E_{\mathcal{D}}[(E_{\mathcal{D}}[\hat{y}] - \hat{y})^2] \\ &= (y - E_{\mathcal{D}}[\hat{y}])^2 + E_{\mathcal{D}}[(E_{\mathcal{D}}[\hat{y}] - \hat{y})^2] \\ &= [\text{błąd obciążenia}^2] + \text{wariancja} \end{aligned} \end{split}\]

W równaniu (5) dużo się dzieje, ale (wbrew pozorom) są to dość podstawowe przekształcenia, wynikające z definicji podstawowych terminów probabilistyki i statystyki.

• Bias (czyli nasz bład obciążenia) uzyskuje definicję:

\[\text{błąd obciążenia} = (y - E_{\mathcal{D}}[\hat{y}])^2\]

, możemy zatem o nim myśleć, jako o średnim błędzie kwadratowym pomiędzy pojeciem docelowym, a wartością oczekiwaną (np. średnią) predykcji różnych modeli dla tego samego zbioru danych.

• Wariancja uzyskuje definicję

  \[\text{wariancja} = E_{\mathcal{D}}[(E_{\mathcal{D}}[\hat{y}] - \hat{y})^2]\]

, możemy zatem o niej myśleć, jako o średnim błędzie kwadratowym pomiędzy średnią predykcją różnych modeli dla tego samego zbioru danych, a predykcją konkretnego modelu.

Znikający wyraz

Uważna Czytelniczka lub Czytelnik stwierdzi, że w (5) w przedostatniej linijce znika wyraz \(E_{\mathcal{D}}[2(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y})].\) Dlaczego tak się dzieje?

Otóż po zastosowaniu operatora wartości oczekiwanej, ten wyraz upraszcza się i skraca do zera. Warto to sprawdzić samemu (słynne: „pozostawiamy to jako ćwiczenie…”). Zachęcam do sprawdzenia samodzielnie tej zależności. W razie czego, poniżej znajduje się jej wyprowadzenie.

Wyprowadzenie odpowiedzi

(6)\[\begin{split} \begin{aligned} E_{\mathcal{D}}[2(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y})] &= 2E_{\mathcal{D}}[(y - E_{\mathcal{D}}[\hat{y}])(E_{\mathcal{D}}[\hat{y}] - \hat{y})] \\ &= 2(y - E_{\mathcal{D}}[\hat{y}])E_{\mathcal{D}}[E_{\mathcal{D}}[\hat{y}] - \hat{y}] \\ &= 2(y - E_{\mathcal{D}}[\hat{y}])E_{\mathcal{D}}[E_{\mathcal{D}}[\hat{y}] - E_{\mathcal{D}}[\hat{y}]] \\ &= 2(y - E_{\mathcal{D}}[\hat{y}])E_{\mathcal{D}}[0] \\ &= 0. \end{aligned} \end{split}\]

Praktyczne zastosowanie

Czy da się to jakoś zastosować w praktyce, albo zbadać za pomocą narzędzi? Owszem. W praktyce, możemy zastosować walidację krzyżową (ang. cross-validation), aby zbadać, jak zmieniają się błąd obciążenia i wariancja w zależności od złożoności modelu.

Ponadto, mamy gotowe biblioteki, które pomagają nam wyznaczać obciążenie i wariancję poszczególnych modeli dla danego zbioru danych / problemu. w ten sposób, możemy wybrać alternatywę, która stanowi rozsądny kompromis.

Przykład

W przykładzie poniżej zbadamy rozkład obciążenia i wariancji kilku modeli dla zbioru danych California housing - zawierającego informacje o cenach nieruchomości w Kalifornii, w zależności od wielu różnych czynników.

import pandas as pd
from tqdm.autonotebook import tqdm
from time import time
from mlxtend.evaluate import bias_variance_decomp
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression

california = fetch_california_housing()
X = pd.DataFrame(california.data, columns=california.feature_names)
y = california.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print(X.shape)

X.head(3)

(20640, 8)

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24

Nasz zbiór danych składa się z 20640 obserwacji i 8 zmiennych objaśniających. Naszym celem jest przewidzenie ceny nieruchomości na podstawie tych zmiennych.

Wykorzystamy pakiet MlXtend oraz zawartą w nim funkcję bias_variance_decomp, która wykonuje następujące działania:

Algorithm 1 (Dekompozycja błędów)

Wejścia

1. Zbiór danych treningowych \(\mathbf{X}\) wraz z wartościami docelowymi \(\mathbf{y}\),

2. Zbiór danych testowych \(\mathbf{X}_{test}\) wraz z wartościami docelowymi \(\mathbf{y}_{test}\),

3. Liczba iteracji próbkowania \(k\),

4. Funkcja kosztu \(L\),

5. Model \(h\)

Wyjście Wyliczenie błędu obciążenia, wariancji i średniej oczekiwanej funkcji kosztu.

1. Dla każdej iteracji \(i\) od \(1\) do \(k\):

   1. Wybierz losowo ze zwracaniem (metodą bootstrap) próbkę ze zbioru treningowego \(\mathbf{X}', \mathbf{y}'\) z \(\mathbf{X}, \mathbf{y}\).

   2. Wytrenuj model \(h\) na zbiorze \(\mathbf{X}', \mathbf{y}'\).

   3. Dokonaj predykcji na zbiorze testowym.

   4. Zapisz różnice pomiędzy predykcją a wartością docelową dla każdej obserwacji.

2. Za pomocą bias-variance-derivation oblicz błąd obciążenia, wariancję i błąd nieredukowalny.

Sprawdźmy zachowanie kilku modeli:

1. Prosta regresja liniowa - oczekujemy najmniejszej wariancji i dużego obciążenia,

2. Pojedyncze drzewo decyzyjne dla regresji - oczekujemy średniej wariancji i średniego obciążenia.

3. Las losowy - oczekujemy małego obciążenia i małej wariancji.

model_results = []

models = [
    ('Linear Regression', LinearRegression()),
    ('Decision Tree', DecisionTreeRegressor(max_depth=10)),
    ('Random Forest', RandomForestRegressor(n_estimators=25, max_depth=10, n_jobs=-1))
]

for name, model in tqdm(models):
    train_start = time()
    avg_expected_loss, avg_bias, avg_var = bias_variance_decomp(
        model, X_train.values, y_train, X_test.values, y_test, 
        loss='mse',
        num_rounds=100,
        random_seed=123)
    train_end = time()
    trianing_time = train_end - train_start
    model_results.append([name, avg_expected_loss, avg_bias, avg_var, trianing_time])

model_results = pd.DataFrame(model_results, columns=['Model', 'Expected Loss', 'Bias', 'Variance', 'Training Time'])
model_results.sort_values('Expected Loss', ascending=True)

	Model	Expected Loss	Bias	Variance	Training Time
2	Random Forest	0.316762	0.294988	0.021775	26.608934
1	Decision Tree	0.456935	0.294924	0.162011	6.042207
0	Linear Regression	0.556295	0.555354	0.000942	0.391138

Widzimy, że nasze obserwacje się potwierdziły:

1. Regresja liniowa - ma największe obciążenie, ale najmniejszą, niemal zerową wariancję.

2. Drzewo decyzyjne - ma średnie obciążenie i wariancję.

3. Las losowy - ma najmniejsze obciążenie i wariancję.

Oczywiście wszystko to jest funkcją złożoności modelu - spójrzmy na czas szkolenia.