Elementy teorii uczenia się

Autor sekcji: dr Filip Wójcik

W niniejszym rozdziale przedstawione zostaną najważniejsze zagadnienia teoretyczne powiązane z teorią COLT - ang. Computational Learning Theory. Jest to dziedzina zajmująca się badaniem algorytmów uczenia maszynowego, ich złożoności obliczeniowej oraz ich zdolności do generalizacji. W ramach tego rozdziału omówione zostaną kluczowe elementy takie jak przestrzeń hipotez, pojecie docelowe i generalizacja.

Pojęcie docelowe i hipotezy

W przypadku uczenia maszynowego, tworząc i szkoląc poszczególne modele, poruszamy się w obszarze dużej niepewności. Warto sobie zadać następujące pytania:

Pytania do procesu uczenia się

1. Skąd mamy gwarancję, że dane, na których uczymy model, są reprezentatywne dla całej populacji?

2. Skąd mamy gwarancję, że etykiety (y) przypisane do danych są poprawne i reprezentatywne dla całej populacji?

3. Skąd wiemy, czy i jaki proces odpowiada w rzeczywistości za przypisywanie etykiet do danych?

Wbrew pozorom, są to bardzo istotne uwagi. Nierzadko zdarza się, że nie wiemy, czy istnieje jakakolwiek zasada, przypisująca etykiety do danych. W takim przypadku, model, który uczymy, może być jedynie zbiorem przypadkowych reguł, które nie mają żadnego związku z rzeczywistością.

Wyobraźmy sobie przez chwilę przestrzeń wszystkich możliwych cech obiektów, oznaczaną jako \(\mathcal{X}\) - jest to wyczerpująca lista wszelkich kombinacji cech, jakie tylko mogą wystąpić w naszych danych. W przypadku filmów, mogą to być takie cechy jak: gatunek, rok produkcji, reżyser, aktorzy, budżet, długość filmu, itd.

Obiekty w tej przestrzeni mają przypisane pewne etykiety - oznaczane jako \(\mathcal{Y}\). W przypadku filmów, mogą to być takie etykiety jak: ocena Filmweb.pl, ocena IMDB, liczba nominacji do Oscara, itd.

Pojęcie docelowe

Zakładamy, że istnieje pewne wyjaśnienie - proces, funkcja, zjawisko (naturalne lub sztuczne), które przypisuje etykiety do obiektów. Tę funkcję nazywamy funkcją docelową albo pojęciem docelowym (ang. target function), oznaczaną jako \(c(x): \mathcal{X} \rightarrow \mathcal{Y}\). [Cic07] [Woj21]

Funkcja docelowa

Niektórzy autorzy (np. [AMMIL12]) posługują się terminem funkcja docelowa zamiast pojęcie docelowe. Funkcja docelowa to funkcja, która przypisuje etykiety do obiektów z zastrzeżeniem, że jest ona zaszumiona - może zawierać błędy, wynikające np. ze złych pomiarów, niedokładności zapisów, niedoprecyzowania pojęć, etc. W kontekście uczenia maszynowego, jest to funkcja, którą staramy się odnaleźć. Funkcję docelową oznacza się jako \(f(x): \mathcal{X} \rightarrow \mathcal{Y}\) [AMMIL12]

Przestrzeń hipotez

Jest to zbiór wszystkich możliwych do wyrażenia przez określony model potencjalnych wyjaśnień danych, mających na celu odnalezienie Pojęcie docelowe. [Cic07] [Woj21]

Algorytm uczenia maszynowego, którego używamy, żeby wyszkolić Model uczenia maszynowego stara się stworzyć uproszczony opis danych, które ma dostępne w taki sposób, aby jak najlepiej odwzorować pojęcie docelowe. W tym kontekście, mówimy o hipotezach: każdy algorytm może tworzyć/reprezentować różne hipotezy, starając się wyjaśnić zależności w danych.

Pytanie brzmi: czy przestrzeń hipotez generowana przez algorytm zawiera w sobie pojęcie docelowe?

Rys. 1 Ilustracja przestrzeni hipotez. Adaptacja za: [Lea97]

Zewnętrzny, duży kwadrat przedstawia całą dziedzinę - przestrzeń wszystkich możliwych wartości atrybutów. Pojęcie docelowe, czyli funkcja, którą chcemy znaleźć, pokrywa część tego obszaru (owal z lewej). Model, tworzony przez określony algorytm może tworzyć różne hipotezy, które są reprezentowane przez owal po prawej stronie. Jak widać - czasem zdarza się, że przestrzeń hipotez nie pokrywa się z pojęciem docelowym: wówczas model „nie trafia” z odpowiedziami. W innych wypadkach - przestrzeń jego hipotez pokrywa się z pojęciem docelowym i wówczas otrzymujemy prawidłowe odpowiedzi.

Przykład - przestrzeń hipotez zawiera pojęcie docelowe

Przyjrzyjmy się zbiorowi danych, prezentowanemu poniżej - każda kropka oznacza obiekt (np. klienta), opisany dwiema cechami numerycznymi (X1, X2 - np. wiek i waga). Każdy obiekt ma przypisaną etykietę (np. czy klient kupił produkt czy nie) - w tym przypadku odpowiadającą kolorowi zielonemu lub niebieskiemu.

Na pierwszy rzut oka wydaje się, że:

1. Pojęcie docelowe istnieje - obiekty po prawej stronie są „niebieskie” a po lewej „zielone”. Istnieje zatem jakiś proces, który przypisuje etykiety do danych i jest to proces sensowny.

2. Przestrzeń hipotez - w tym przypadku, przestrzeń hipotez jest bardzo prosta: wystarczy narysować linię, która oddzieli obiekty zielone od niebieskich. Wówczas, model, który stworzy taką hipotezę, będzie w stanie poprawnie klasyfikować nowe obiekty.

Show code cell source Hide code cell source

X_sep, y_sep = make_blobs(
    n_samples=100, centers=2, n_features=2, center_box=(0, 10), random_state=123
)
plt.scatter(X_sep[:, 0], X_sep[:, 1], marker="o", c=y_sep, s=25)
sns.scatterplot(x=X_sep[:, 0], y=X_sep[:, 1], hue=y_sep, palette="viridis")
plt.xlabel("Cecha 1 - X1")
plt.ylabel("Cecha 2 - X2")
plt.title("Liniowo separowalne obiekty");

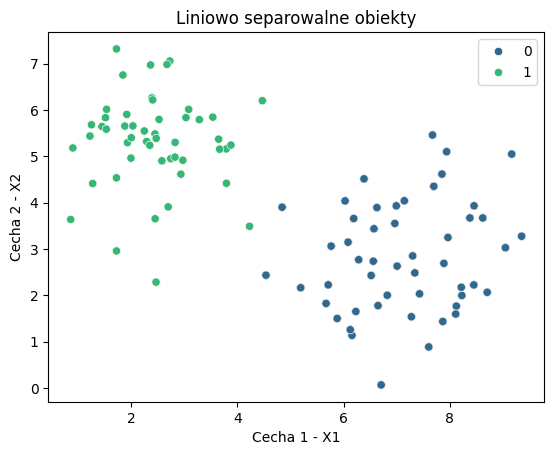
Możemy teraz wyznaczyć kilka linii oddzielających od siebie obie strefy. Każda taka linia (formalnie: model liniowy) jest hipotezą - czyli próbą wyjaśnienia zależności w danych.

Ewidentnie jedne są lepsze od innych.

Show code cell source Hide code cell source

def make_line_from_coef(X_data: np.array, coef: np.array, intercept: np.array, col: str, ax: plt.Axes):
    # Create a range of values for x1
    x1_vals = np.linspace(X_sep[:, 0].min(), X_sep[:, 0].max(), 100)
    # Calculate the corresponding x2 values
    x2_vals = -(coef[0] * x1_vals  + intercept) / coef[1]
    line_label = f"{coef[0]:.2f}x1 + {coef[1]:.2f}x2 + {intercept[0]:.2f} = 0"
    ax.plot(x1_vals, x2_vals, color=col, linestyle='--', label=line_label)


coefs = [
    (np.array([4.87]), np.array([-5,  1.5]), 'red'),
    (np.array([4.87]), np.array([-5,  2.5]), 'pink'),
    (np.array([4.87]), np.array([-5,  5.5]), 'purple'),
    (np.array([4.87]), np.array([-5,  6.5]), 'black'),
]


fig1, ax = plt.subplots()
for intercept, coef, col in coefs:
    make_line_from_coef(X_sep, coef, intercept, col, ax)

plt.xlabel("Cecha 1 - X1")
plt.ylabel("Cecha 2 - X2")
plt.legend()
plt.title("Próba dopasowania modeli liniowych");

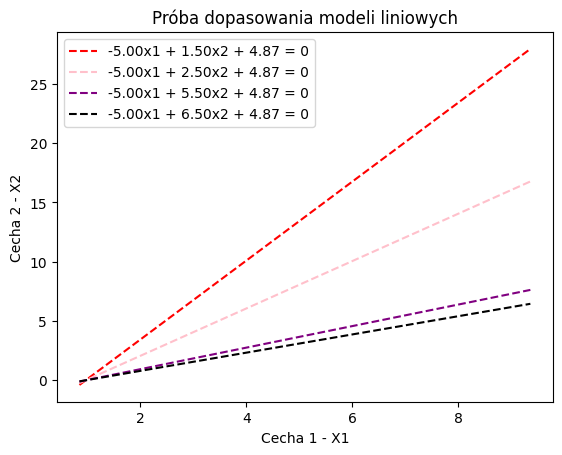
Jeśli pozwolimy modelowi liniowemu nauczyć się własności danych - znajdzie on w swojej przestrzeni hipotez najlepsze rozwiązanie, które oddzieli punkty od siebie.

Możemy to przedstawić jak na obrazku poniżej, gdzie model tworzy płaszczyznę decyzyjną - linię, która oddziela obiekty zielone od niebieskich.

Show code cell source Hide code cell source

lr1 = LogisticRegression()
lr1.fit(X_sep, y_sep)
fig, ax = plt.subplots()
display = DecisionBoundaryDisplay.from_estimator(
    lr1,
    X_sep,
    response_method="predict",
    xlabel="Cecha 1 - X1",
    ylabel="Cecha 2 - X2",
    ax=ax,
)
sns.scatterplot(x=X_sep[:, 0], y=X_sep[:, 1], hue=y_sep, palette="viridis", ax=ax)
plt.show()

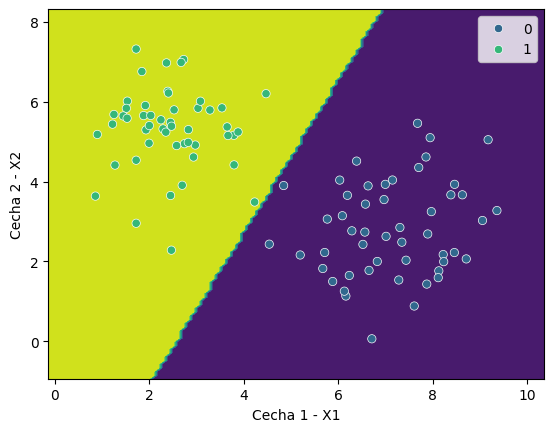
Przykład - pojęcie docelowe poza przestrzenią hipotez

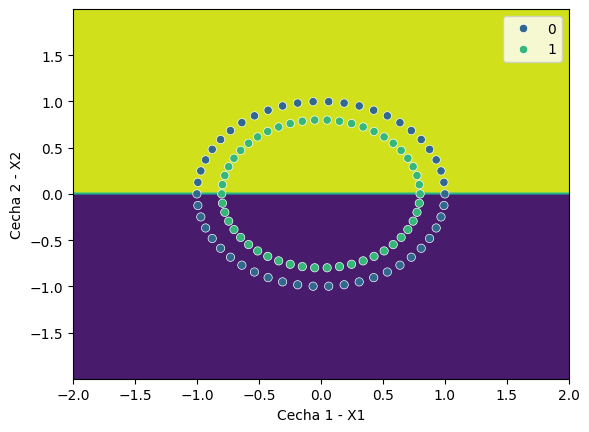
Rozpatrzmy kolejny przykład - bardzo niekorzystny dla naszego algorytmu liniowego. Także i tym razem mamy zbiór danych, opisany dwiema cechami numerycznymi (X1, X2) i etykietami (zielony, niebieski).Poszczególne etykiety (klasy) układają się w okrąg - co sugeruje, że nie istnieje żadna prosta, która oddzieliłaby obiekty jednej klasy od drugiej.

Show code cell source Hide code cell source

X_circ, y_circ = make_circles(random_state=42)

sns.scatterplot(x=X_circ[:, 0], y=X_circ[:, 1], hue=y_circ, palette="viridis");
plt.title("Obiekty nieseparowalne liniowo");

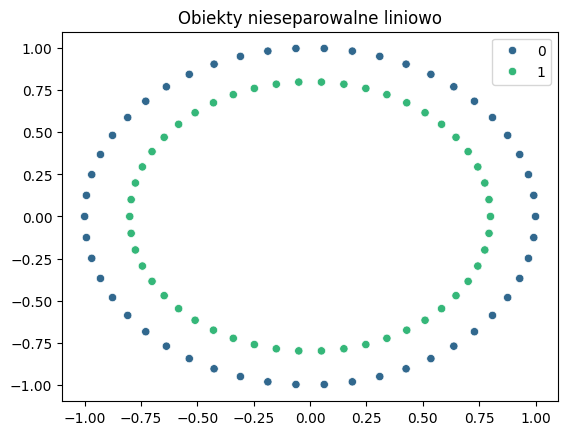
Choćbyśmy dopasowali nie wiadomo jak dobry model liniowy nie ma on najmniejszych szans sensownie oddzielić od siebie tych obiektów. W najlepszym wypadku, połowa obiektów każdej klasy znajdzie się po niewłaściwej stronie.

Show code cell source Hide code cell source

lr2 = LogisticRegression()
lr2.intercept_ = np.array([[0.0]])
lr2.coef_ = np.array([[0.0, 1.0]])
lr2.classes_ = np.array([0, 1])
fig, ax = plt.subplots()
display = DecisionBoundaryDisplay.from_estimator(
    lr2,
    X_circ,
    response_method="predict",
    xlabel="Cecha 1 - X1",
    ylabel="Cecha 2 - X2",
    ax=ax,
)
sns.scatterplot(x=X_circ[:, 0], y=X_circ[:, 1], hue=y_circ, palette="viridis", ax=ax)
plt.show()

Elementy składowe procesu uczenia się

Mając na uwadze powyższe, możemy wskazać na diagramie najważniejsze elementy, składające się na proces uczenia się.

Rys. 2 Składowe procesu uczenia się. Adaptacja za: [MRTB12]

Co dokładnie mamy na tym diagramie? Wszystkie elementy wymienione do tej pory. Po kolei:

1. Nieznana nam funkcja prawdopodobieństwa \(P(x)\) odpowiada za losowanie przykładów. Innymi słowy: model uczy się na próbce całej populacji. Próbki są wybierane, a o tym, które trafią nam w ręce decyduje właśnie rozkład \(P(x)\).

2. Nieznana funkcja docelowa lub pojęcie docelowe nadaje etykiety do obiektów. W przypadku klasyfikacji, jest to funkcja, która przypisuje obiektom klasy. To właśnie tej funkcji staramy się nauczyć, albo przybliżyć. Przykłady przytaczaliśmy już wcześniej: co decyduje o tym, że jedne osoby mają powikłania po chorobie C a inne nie?, co decyduje o wzroście/spadku cen akcji?, co decyduje o tym, że klient kupi produkt?.

3. Zbiór uczący się składa się z par: \(\mathbf{x}_i, y_i\), czyli zestawu macierzy atrybutów i etykiet.

4. Wybieramy algorytm uczenia maszynowego, który posiada pewną przestrzeń hipotez \(\mathcal{H}\) - jest to jego zdolność do wyrażania różnych zależności w danych. Przykład: model liniowy omówiony wcześniej - przestrzenią hipotez są wszystkie możliwe do narysowania proste linie.

5. Model uczy się, starając się jak najlepiej dopasować do posiadanych etykiet przykładów. Na końcu otrzymujemy hipotezę docelową \(h\). Mamy nadzieję, że dobrze przybliża ona pojęcie docelowe.

Tym co steruje procesem uczenia się i oceną jego jakości jest błąd generalizacji:

Błąd generalizacji

Mając daną hipotezę \(h \in \mathcal{H}\), oraz pojęcie docelowe \(c \in \mathcal{C}\) oraz rozkład danych \(D\) z którego pochodzą przykłady uczące, błąd generalizacji jest średnim prawdopodobieństwem, że hipoteza \(h\) będzie błędna na losowym przykładzie \((x, y)\) zgodnie z rozkładem \(D\). Formalnie:

\[R(h) = P_{(x \sim D)} \left[h(x) \neq c(x)\right] = \mathbb{E}_{x \sim D} \left[\mathbb{I}_{h(x) \neq c(x)}\right]\]

gdzie \(\mathbb{I}\) jest funkcją indykatorową (wskaźnikową), która przyjmuje wartość 1, gdy warunek wewnątrz jest spełniony, a 0 w przeciwnym wypadku. [MRTB12]

Z powyższych, dość mocno teoretycznych (jak dotąd) rozważań, wysuwa się jeden, bardzo istotny dla wszystkich praktyków uczenia maszynowego wniosek:

Uczenie maszynowe jako probabilistyczne poszukiwanie hipotez

W tym ujęciu, uczenia maszynowego widać, jak mocno niepewny i stochastyczny jest to proces. Niepewność pojawia się w kilku miejscach:

• Po pierwsze - przykłady uczące są wybierane losowo z populacji, co oznacza, że nie mamy pewności, czy są one reprezentatywne.

• Po drugie - etykiety przypisane do danych mogą być błędne, niepełne, lub nieodpowiednie.

• Po trzecie - przestrzeń hipotez, w której poruszamy się, może nie zawierać w sobie pojęcia docelowego.

• Po czwarte - model, który tworzymy na bazie algorytmu PRZESZUKUJE przestrzeń swoich hipotez próbując się dopasować do posiadanych danych uczących.

Warto mieć te elementy na uwadze, gdy klienci, kontrahenci lub osoby chcące otrzymać od nas wyniki, pytają o pewność naszych modeli. Warto wtedy zwrócić uwagę na to, że nie ma pewności - są jedynie prawdopodobieństwa.

Obciążenie indukcyjne

Podczas wyboru najlepszego algorytmu, który posłuży nam do zbudowania modelu, naturalnym jest, że staramy sie wybrać taki, który ma jak najmniejszy błąd generalizacji. Warto w ramach tego procesu rozważyć mocne i słabe strony każdego z algorytmów, które bierzemy pod uwagę. Jak widzieliśmy we wcześniejszych przykładach, może się zdarzyć tak, że próbujemy zastosować narzędzie absolutnie nieprzystosowane do naszego problemu - np. model liniowy do rozdzielenia obiektów w kształcie okręgu.

Istnieje kilka pojęć, które posłużą nam do zdefiniowania tak rozumianych ograniczeń i możliwości algorytmów uczenia maszynowego.

Obciążenie indukcyjne

Zbiór założeń i ograniczeń algorytmu, sprawiający, że stawiane przez niego hipotezy różnią się od pojęcia docelowego lub skłaniające do preferowania jednej hipotezy nad inną, nazywane są zbiorczo obciążeniem indukcyjnym. [Cic07] [Woj21]

Innymi słowy - Obciążenie indukcyjne mówi nam o wszystkich czynnikach, które wpływają na to, dlaczego dany algorytm lub model, podejmuje takie decyzje, jakie podejmuje.

Obciążenie indukcyjne występuje w dwóch najczęstszych postaciach: reprezentacji i preferencji.

Obciążenie reprezentacji

Informuje o tym, jak ograniczona jest przestrzeń hipotez, które ma do dyspozycji określony algorytm. Innymi słowy – definiuje zawężenie funkcji wyjaśniających, których system może używać do wyjaśniania zjawisk. Ten rodzaj obciążania nie daje się w łatwy sposób wyeliminować - jest bowiem wpisany w samą strukturę algorytmu. [Cic07] [Woj21]

Obciążenie preferencji

związane jest z heurystykami wyboru najlepszej hipotezy spośród generowanych (proponowanych) przez algorytm. Funkcje te mogą zostać zaprojektowane z użyciem takich założeń lub aparatu matematycznego, iż prowadzić będą w sposób systematyczny i powtarzalny do preferowania określonych wyborów ponad innymi. [Cic07] [Woj21]

Brzmi skomplikowanie? Rozważmy kilka przykładów.

Ćwiczenie - obciążenie indykcyjne

Zastanów się nad następującymi przykładami ograniczeń posiadanych przez algorytmy i modele. Które z nich dotyczą preferowania pewnych wyników, a które wpisane są w samą strukturę algorytmu/modelu?

Model liniowy nie jest w stanie oddzielić danych w postaci dwóch okręgów.

Obciążenie reprezentacji. To jest prosty przykład. Model rysujący proste linie nie może reprezentować swoich hipotez w inny sposób.

Model K-najbliższych sąsiadów nadaje najwyższą wagę atrybutom wyrażonym w największych jednostkach.

Obciazenie preferencji. Modele oparte na analizie odległości między obiektami są podatne jednostkę, w jakiej wyrażane są cechy. Problem ten można rozwiazac odpowiednio skalując przykłady.

W przypadku silnej nierównowagi klas (np. 95% zdrowych osób, 5% chorych) model zawsze przewiduje klasę większościową.

Obciążenie preferencji. W przypadku, gdy obydwu klasom nadajemy taką samą wagę, nic dziwnego, że przy zaburzonej liczności, modelowi najbardziej „opłaca się” przewidywać klasę najczęstszą.

Sieć neuronowa typu Multi-Layer-Perceptron nie może przetwarzać danych w postaci grafowej.

Obciążenie reprezentacji. Zwykła sieć neuronowa nie jest w stanie, natywnie, przetwarzać danych grafowych. Do tego celu potrzebujemy dedykowanych modeli np. sieci MPNN GNN (message passing graph neural networks).

Przykład obciążenia indukcyjnego - obciążenia reprezentacji

Ograniczenie reprezentacji przez model liniowy, w przypadku danych układających się w kształt okręgów widzieliśmy już wcześniej. Zobaczmy teraz, jak poradzi sobie np. drzewo decyzyjne dla tego samego zbioru, w zależności od swojej konfiguracji - głębokości.

Show code cell source Hide code cell source

def build_dt(**kwargs):
    return DecisionTreeClassifier(**kwargs)

def fit_estimator_and_plot(builder_func, X: np.array, y: np.array, title: str, ax=None, **kwargs):
    model = builder_func(**kwargs)
    model.fit(X, y)
    if ax is None:
        fig, ax = plt.subplots()
    display = DecisionBoundaryDisplay.from_estimator(
        model,
        X,
        response_method="predict",
        xlabel="Cecha 1 - X1",
        ylabel="Cecha 2 - X2",
        ax=ax,
    )
    sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette="viridis", ax=ax)
    ax.set_title(title)

Proste drzewo o głębokości 2 jest niewiele lepsze od modelu liniowego.

Show code cell source Hide code cell source

fit_estimator_and_plot(build_dt, X_circ, y_circ, "Drzewo głębokość = 2", max_depth=2)

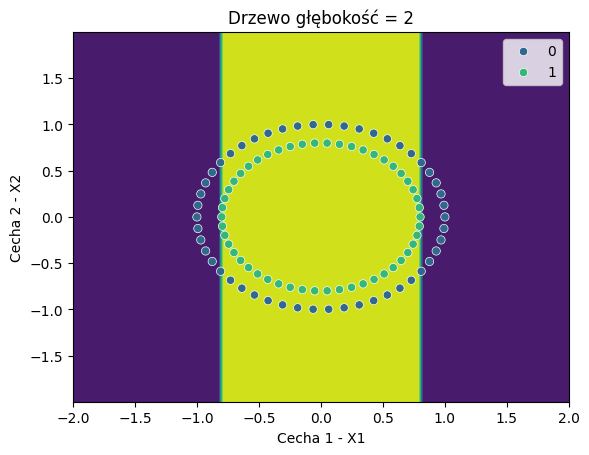
W miarę zwiększania głębokości drzewa, widzimy, że stopniowo coraz lepiej radzi sobie z podziałem danych.

Show code cell source Hide code cell source

fig, axs = plt.subplots(1, 5, figsize=(20, 10))
for idx, depth in enumerate([1, 2, 4, 8, 20]):
    fit_estimator_and_plot(build_dt, X_circ, y_circ, f"Drzewo głębokość = {depth}", max_depth=depth, ax=axs[idx])
plt.show()

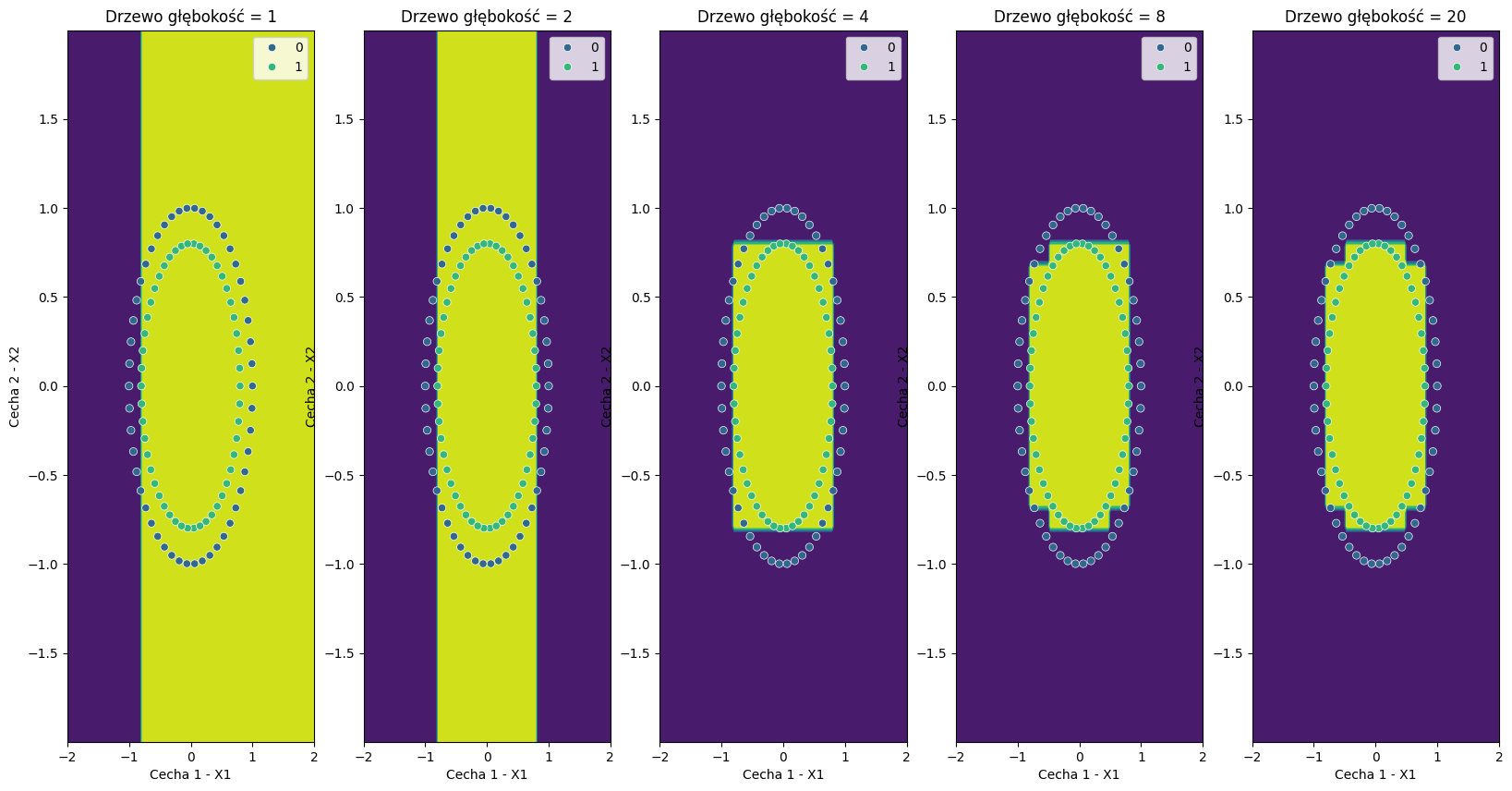
Drzewo o głębokości 8, co prawda, nie jest w stanie idealnie oddzielić obiektów, ale już znacznie lepiej niż model liniowy.

Zwiększenie głębokości drzewa do 20 nijak nie poprawia jednak trafności - zachodzi tu więc niewielkie obciążenie reprezentacji.

Zobaczmy jednak, co się stanie, jeśli wyszkolimy model, który otrzyma bardziej złożoną przestrzeń cech - cechy X1 i X2, podniesione do kwadratu i kolejnych potęg, a także przekształcone wielomianowo.

Show code cell source Hide code cell source

def build_poly_dt_pipeline(**kwargs):
    pipeline = Pipeline([
        ("poly", PolynomialFeatures(degree=4, interaction_only=False)),
        ("dt", DecisionTreeClassifier(**kwargs))
    ])
    return pipeline

fig, axs = plt.subplots(1, 4, figsize=(20, 10))
for idx, depth in enumerate([1, 2, 4, 8]):
    fit_estimator_and_plot(build_poly_dt_pipeline, X_circ, y_circ, f"Drzewo wielomianowe głębokość = {depth}", max_depth=depth, ax=axs[idx])
plt.show()

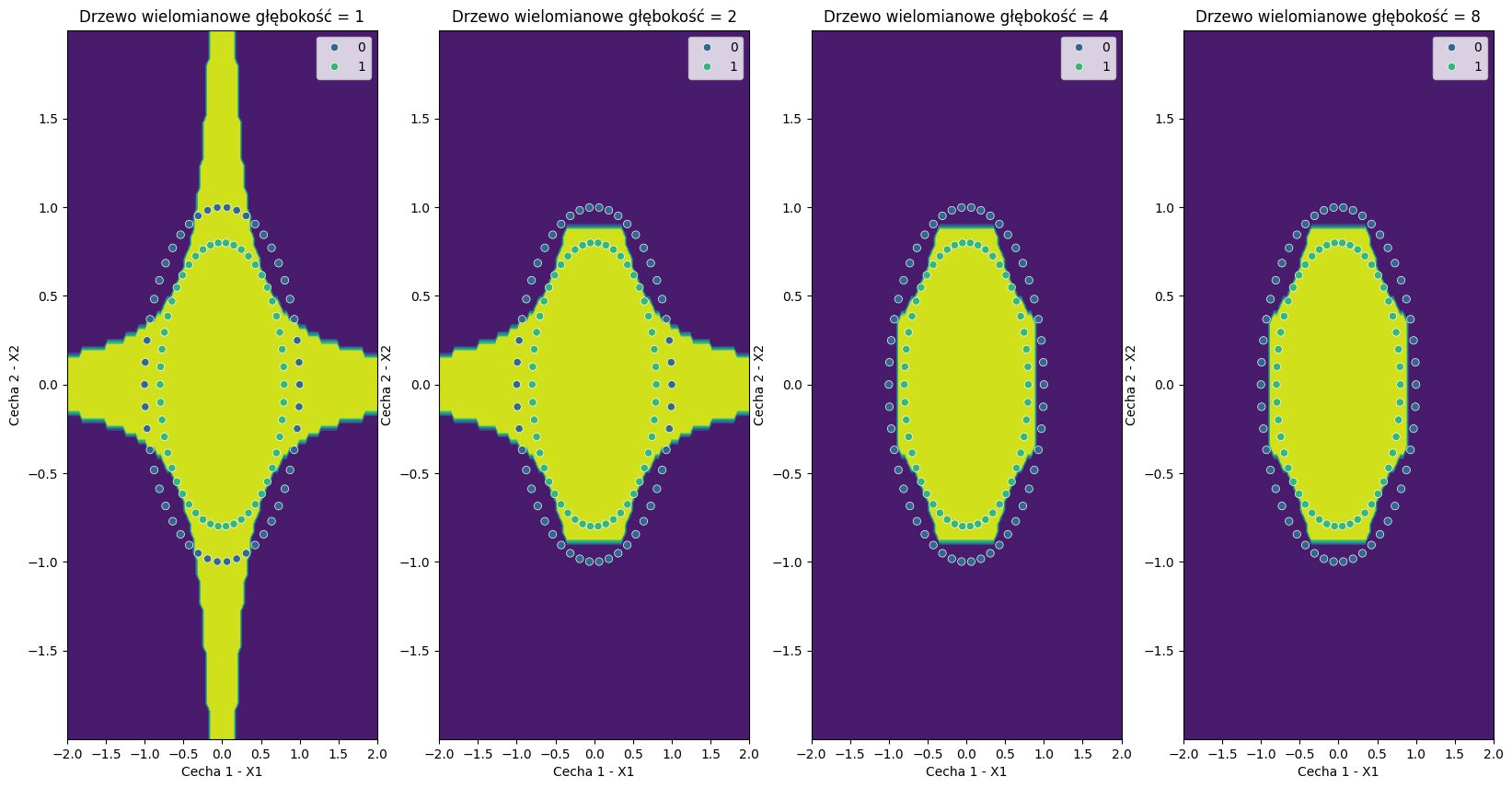
Widać, że w tym przypadku trafność znacznie się poprawiła już przy głębokości drzewa = 4. Tym samym znieśliśmy ograniczenie reprezentacji drzewa, poprzez wzbogacenie danych źródłowych. Jest to częsta strategia działania - nierzadko wystarczy zmienić format oryginalnych danych lub je przekształcić, by otrzymać lepsze wyniki.

PAC-nauczalność

Tak silna obecność niepewności i elementów probabilistycznych doprowadziła do sformułowania pojęcia PAC-nauczalności (ang. Probably - Approximately - Correct learning). Formalna definicja przedstawia się następująco:

PAC-nauczalność

Klasa pojęć \(\mathcal{C}\) jest PAC-nauczalna, jeśli istnieje algorytm \(\mathcal{A}\) i funkcja wielomianowa \(poly(\cdot, \cdot, \cdot, \cdot)\) taka, że dla dowolnego \(\epsilon \gt 0\) oraz \(\delta \gt 0\) dla wszystkich rozkładów prawdopodobieństwa \(D\) dla zbioru obiektów \(\mathcal{X}\) i dla każdego pojecia docelowego \(c \in \mathcal{C}\) zachodzi następująca zależność dla próbki o wielkości $\(m \geq poly\left(\frac{1}{\epsilon}, \frac{1}{\delta}, \text{rozmiar}(\mathcal{X}), \text{złożoność}(\mathcal{C})\right)\):

\[P_{S \sim D^m} \left[R(h_S) \leq \epsilon\right] \geq 1 - \delta\]

gdzie \(h_S\) to hipoteza wygenerowana przez algorytm \(\mathcal{A}\) na podstawie próbki uczącej \(S\) o rozmiarze \(m\), a \(R(h_S)\) to błąd generalizacji hipotezy \(h_S\). [MRTB12]

Efektywna PAC-nauczalność

Jeśli algorytm \(\mathcal{A}\) działa w czasie \(poly(\cdot, \cdot, \cdot, \cdot)\), to klasa pojęć \(\mathcal{C}\) jest efektywnie PAC-nauczalna. [MRTB12]

Powyższe definicje mogą się początkowo wydawać skomplikowane, ale ich znaczenie jest de facto dość proste.

PAC-nauczalność, czyli co?

PAC-nauczalność oznacza, że dla dowolnego pojęcia docelowego \(c\) z klasy \(\mathcal{C}\), istnieje algorytm \(\mathcal{A}\), który potrafi nauczyć się tego pojęcia, a prawdopodobieństwo, że popełni błąd mniejszy niż \(\epsilon\) wynosi co najmniej \(1 - \delta\). W praktyce oznacza to, że mamy pewność, że nasz model jest w stanie nauczyć się pojęcia docelowego z pewnym prawdopodobieństwem. Kluczowe staje się zwrócenie uwagi na znaczenie poszczególnych słów ze skrótu PAC. Zrobimy to w kolejności zgodnej z intuicyjnym zrozumieniem:

1. Approximately (w przybliżeniu) - model nie musi być idealny, ale musi być blisko prawdy. O tym, jaki błąd jest dopuszczalny mówi parametr \(\epsilon\). Na przykład, jeśli zakładamy \(\epsilon = 0.05\), to oznacza, że model może popełnić błąd w 5% przypadków.

2. Probably (prawdopodobnie) - mówi o tym, jakie jest prawdopodobieństwo, że model popełni błąd mniejszy niż \(\epsilon\). O tym decyduje parametr \(\delta\). Na przykład, jeśli zakładamy \(\delta = 0.01, 1-\delta = 0.99\), to oznacza, że mamy 99% pewności, że nasz model popełni błąd nie większy niż \(\epsilon\) (w tym przypadku: 5%).

3. Correct (poprawny) - model musi być poprawny, czyli musi być w stanie nauczyć się pojęcia docelowego, a zatem minimalizuje błąd generalizacji.

Jak widzimy, najlepsze, co możemy dostać w przypadku PAC-nauczalności, to założenie, że model nie popełni błędu większego niż założony \(\epsilon\), nie częściej niż z prawdopodobieństwem \(\delta\).

Takie ujęcie uczenia maszynowego jest dość daleko od pragnienia posiadania zawsze idealnych, albo prawie idealnych modeli, które działają poprawnie. W praktyce, mamy do czynienia z nieredukowalnym ryzykiem i niepewnością.

Dodatkowym aspektem, obecnym w przestawionej definicji jest wielkość próbki uczącej m oraz, na razie niezdefiniowana, funkcja wielomianowa decydująca o czasie wykonywania algorytmu.